Materials

Introduction

Material properties are physical ones and in order to understand them you need to understand the physical terms they are based on. Since there are at least some of you who are currently taking Physics for the first time, I need to introduce you to some vocabulary. I am not going to be getting too deep into the meanings since that is what your Physics class is for, but I do need you to be aware prior to when it is covered elsewhere. Additionally, I will be discussing some terms that are beyond the basics Physics courses, and I will be spending a little more time with those, but it is not necessary that you fully understand them at this point in your college career. You will see them again.

Furthermore there will be material properties that I do not discuss since they are not relevant to this course, or even the construction industry as a whole. These properties will be introduced (if at all) in your courses on Physics and Chemistry (if you take it).

Units of Measure

Just to preemptively clarify the meaning of some of the units and abbreviations, I'm going to be using I'm listing them here along with their definitions. I'm not defining many of the metric units since I'm not going to be using them frequently in examples and you will be learning all about them in Physics.

Distance	Force	Pressure
in - inches ft - feet mm - millimeters m - meters	lb or lbs - pounds kips - 1,000 pounds N - Newtons kN - 1,000 Newtons	psi - pounds per square inch $\left(\frac{lb}{in^2}\right)$ Pa - Newtons per square meter $\left(\frac{N}{m^2}\right)$ ksi - kips per square inch $\left(\frac{kip}{in^2}\right)$ kPa - kiloNewtons per square meter $\left(\frac{kN}{m^2}\right)$

Material Properties

The physical quantities that are used define material properties, from a usability point of view, can mostly be developed from two physical quantities, force and length or distance. An example of force is weight. It is the quantity that can cause an object to begin to move. Another property of Physics is energy and for what we will be looking at energy can be thought of as a force being applied continuously over a distance. So if force is $F$ and distance is $L$ then energy is just $E = F \times L$. There are other ways to calculate energy but the units of energy always work out to be a force unit times a distance unit, i.e. foot-pounds or Newton-meters. This is also the same units as work $W$, and in some sense they are just different sides of the same coin. Since $E$ is reused for other values I will generally use $W$ when referring to energy, though I will try to point this out every time.

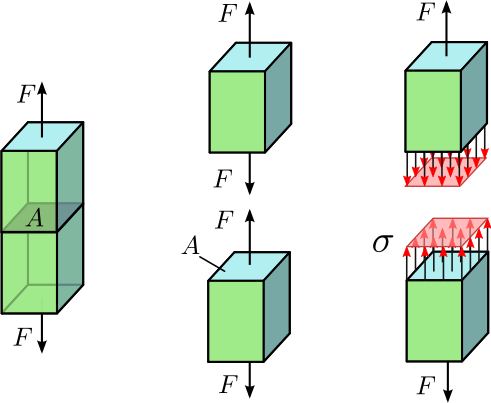Stress is used frequently when describing material properties. Stress is a pressure measurement and pressure is just a force divided by the area it is applied over. Stress is referred to by several different variable depending on the context. In Physics it will probably be introduces as $\sigma$ (sigma). However in construction you will see it in several forms, $\sigma$ for stress perpendicular to a plane known as normal stress or axial stress, and $\tau$ (tau) for stress parallel to a plane known as shear stress. There are even more specific versions of these for specific materials like $f_b$ in timber for normal stress due to bending, $f_c$ for normal stress due to axial compression, $f_t$ is the axial stress due to tension, $f_v$ is the shear stress, and there are others. The point is that it is a very common property.

There is a physical law you will learn about that I'm sure you have already heard of, "for every action there is an equal and opposite reaction". This can be used to relate another material property to stress, and that is strain. Stepping back a moment if I apply a force to down on a spring on a table how does this apply? Unless the spring is moving then it must be pushing back on me. How does it accomplish this? It deforms a little; it store up the energy I used compressing it. This energy remains stored until I release the spring. How does this relate to the material property of stain? Strain is change in length divided by original length. Strain, however, does not refer to springs but rather solid material. If instead of a spring I have a block of aluminum on the table, when I pushed down on it it would ever so slightly change in length like the spring. If this change in length in the aluminum is divided by the block's original length, it is know as the strain in the aluminum and the symbol is $\varepsilon$ (epsilon or sometimes $\epsilon$).

The units of strain are a little unusual, $\left(\tfrac{\text{length}}{\text{length}}\right)$, and these should cancel out. However just to be clear when writing values for strain this fraction is often not simplified. You will see units of $\tfrac{\text{in}}{\text{in}}$, or $\tfrac{\text{mm}}{\text{mm}}$ written out in calculations. This helps the reader understand that this is a measure of strain and not just a constant.

There are other versions of strain which have different symbols like shear stain ($\gamma$) but for this class $\varepsilon$ is as much as you need to be aware of.

With these terms discussed we can now cover the rest of the physical properties that you need to know.

Young's Modulus

%matplotlib inline
%run Modulus.py

Young's modulus or elastic modulus was named after British scientist Thomas Young. Young was not the first to work with the elastic modulus but he was the first to widely publicize it. The elastic modulus is also denoted with $E$ (though you may see $Y$ in Physics). Since the elastic modulus is used substantially more often in describing material properties you should assume that if you see $E$ that is what I am referring to. If I absolutely must use $E$ to refer to energy I will be sure to point it out.

Now back to the elastic modulus. The elastic modulus is just the ratio of how much stress is required to produce a given amount of strain in a specific material.

$$\text{Elastic modulus} = \frac{\text{Stress}}{\text{Strain}}$$$$\text{or just}$$$$E = \frac{\sigma}{\varepsilon}$$

For a most material there is a range over which there is the linear relationship between stress and strain.

$$\sigma = E \times \varepsilon$$$$or$$$$\varepsilon = \frac{\sigma}{E} $$

The elastic modulus of steel is $29,000,000\text{ psi}$. Below I've plotted the elastic region of A36 steel to demonstrate the relationship.

modulus("yield")

The limit to the elastic behavior in a metallic material is know as the yield point.

Plastic Behavior

We will be studying about plastic in this course however the term "plastic behavior" refers to how some metals behave after reaching their yield point. Once the yield point is reached the material (steel in this case) will continue to strain (or deform) without the addition of any more stress. This continuous deformation is what is known as plastic behavior. This can occur to a much greater stain than the level of stain at the yield point. The figure shows the what limit of this purely plastic region is for A36 steel.

modulus('plastic')

This is a really desirable behavior. If a beam is about to collapse, if it have a plastic range, then it will substantially deform before its ultimate failure. This can be thought of as a early warning before collapse. The tendency of a material to undergo plastic deformation is known as its ductility. A material like steel is very ductile. A material that has very low or no ductility is known as brittle. A piece of chalk is brittle. If you try to bend it, it will not visibly deform before it breaks. If you used big enough pieces of chalk you could build a building out of it, but you would have no warning if you were overloading the structure. No one would want to use it, out of fear that it could collapse at any time.

Ultimate Strength

The point at which a material cannot have any additional stresses applied to it, without failure, is known as that material's ultimate strength. Some metals, like some types of steel, will actually start to strengthen after the plastic limit. This is known as strain hardening. It is one way that versions of steel are made stronger. In the figure a complete idealized stress-strain relationship for A36 steel is shown.

modulus('ultimate')

Up until to this ultimate limit there is one other important behavior that occurs. If the stress is removed, the strain would not go back down to zero. Rather the reduction of stress and strain would be parallel the elastic portion of the graph. The deformation that remained, once the stress reaches zero is known as the permanent set. In this figure, at this scale, the path of stress removal would just about be a vertical line straight up and down. This would mean that the permanent set is about $ 0.20 \frac{in}{in}$, at the ultimate stress. Any re-loading on the sample would casue the stress to go right back up that line, displaying the same elastic modulus but not display the previously seen plastic behavior.

Energy Absorption - Toughness

Toughness is a measure of how much energy can be absorbed by a volume of material before it fails. Energy, as you remember, has units of force times distance. It can be calculated by finding the area under the ultimate stress-strain curve down to the strain axis. This may be an odd concept, finding the area of a shape who's sides have different units. When trying to understand it first just think of a rectangle that has units of $\frac{in}{in}$ on one side and units of $psi$ on the other. The units are just another part of each sides length. As such you just need to multiply the units together to find the units of the area. In this case $\frac{in}{in}\times psi$.

Rather than going through a complicated calculation to prove that, let's just look and see that the units of energy per volume work out to be the same as the units of stress times strain. This may be something you have never seen before but it is a quick way to check if a calculation is possibly right. If you assume all the numerical values in a problem, are all one but leave the units in place you should be able, through algebraic manipulation, to prove or disprove, that both sides of an equation have the same units. If it works out, it doesn't prove that the equation is right, but if it doesn't work out then it does prove the equation is wrong. This is known as unit analysis.

Let's set up the variables first and assume we are working in imperial units. $$\varepsilon \times\sigma = \frac{W}{V} $$

where

• $\varepsilon$ - strain $\left(1 \frac{in}{in}\right)$
• $\sigma$ - stress $(1 psi)$
• $W$ - Work or Energy $(1 in \times lb)$
• $V$ - Volume $(1 in^3)$

Let's substitute the the units in for the variables. Since we are assuming all the numerical values are one we don't have to write them out.

$$\frac{in}{in}\times psi = \frac{in \times lb}{in^3} $$

Replace $psi$ with its definition. $$\frac{in}{in}\times \frac{lb}{in^2} = \frac{in \times lb}{in^3} $$ Multiple through... $$\frac{in \times lb}{in \times in^2} = \frac{in \times lb}{in^3} $$ Simplify... $$\frac{in \times lb}{in^3} = \frac{in \times lb}{in^3} $$ The units match. Again, this isn't a proof but it does show that the answer should be in the correct units when the calculation is done. You will need more Physics and probably a little Calculus before I can show you the real proof. For now just take my word for it, or read up on it here. FYI $\int$ is a mathematic symbol for finding the area under a curve.

Fracture Point

The point of ultimate stress and strain of a material is known as its fracture point. This is when the material actually reaches failure. Depending on how you are determining the usable strength of a material, you may or may not need to know this value. If you plan to only use a material in the elastic range of its behavior then you won't need to know about this ultimate limit. However, if you are designing something that is allowed to suffer some damage when in use, then this is a point on the stress-strain diagram you will need to know about.

Just so you know, most structures are designed now days with the expectation that they will suffer some damage in their life time. It turns out that it is much cheaper to build this way.

Rupture

If a ductile material in a structure has reached its fracture point and fails, the failure is called a rupture. This is actually a complicated concept that has many aspects. Due to that I may just leave it for a future course. However I may briefly discuss necking and rupture in the Steel lecture.

Shear Failure

From one point of view shear failure may be the easiest to understand. If a material is subjected to a shear force, the material may fail in shear. In future courses you will learn about the complexities of this failure mode but for now you can just think of it is a failure due to being sheared.

The image below is of idealized deformation due to an applied shear stress ($\tau$). Failure occurs when shear strain $\left(\gamma = \frac{\Delta l}{l} \right)$is excessive.

There is such a thing as the shear modulus $\left(G = \frac{\tau}{\gamma}\right)$ but since it has a relationship with the elastic modulus, it is seldom calculated separately. $$G = \frac{E}{2(1+\nu)}$$ The one term in that equation you might not be familiar with is $\nu$ (nu) which is the symbol for the Poisson's ratio. It is a measured constant like the elastic modulus and just represents the amount that a material expands laterally when it is compressed axially. For context, a material that is non-compressible, i.e. does not change volume when compressed, will have a Poisson's ratio of 0.5. The reason for this is that 50% of the material that is displaced due to vertical compression goes to the left and right while the other 50% pushes out the front and back. Rubber is an example of a material that has a Poisson's ratio very close to 0.5. In contrast steel has a Poisson's ratio in the range of 0.25 to 0.3 (it plays a role in necking).

Deformations

Excessive deformation can be another type of failure. A material can be strong enough for the intended use case but still will be inadequate due to excessive deflections. Consider the following. If you made a second story floor out of rope, it may very well be strong enough, however the amount or movement it would undergo when anyone tried to walk on it would render it unusable for any office work.

That is a little extreme, but there are other reasons, like the brittleness of an attached component that may require limiting the deformations of a material. Again, I'll leave further explanation for later courses.

Buckling

Buckling is less of a material failure mode and more of a failure due to geometry but I thought I would mention it here since I am talking about failure modes. However bucking is partially due to some of the material properties I've already listed, like the elastic modulus.

Either way I wanted it to be in your vocabulary even if you are not going to be learning more about it for a couple of years.

Compression

One related mode of failure is crushing due to compression. Crushing occurs when an element is short enough that it cannot buckle and the material strength is inadequate to prevent permanent deformation. The deformation can be localized to the point of contact or it can be through the element. We will get more into compressive failure when we look at concrete.

(Spoilers: Though the failure mode most commonly associated with concrete overloading is compression, concrete compression failure is actually a form of tension failure.)

Connections

Connections can fail due to both geometric and material failures. Examples of these include slip failure and bearing failure. Slip failure is when a bolted connection allows the two connected elements to slide relative to each other. Bearing failure occurs when the material pressing against the fasteners in a connection fails by deforming, and allowing the connected elements to move relative to each other. There are obviously other types of connection failures, like the fasteners themselves could be sheared off by the connected elements, or the material surrounding a fastener could tear away from the main portion of an element in a rupture type of failure.

One of the most famous connection failures was the Hyatt Regency walkway collapse. The connection supporting the walkways was changed from the original design which resulted in a much weaker connection. It resulted in the death of 114 people and 216 more injured. It was a failure of both material and geometry.

Summary

To sum up, this is an overview of some of the material properties that we'll be seeing this semester. This is not a complete list, nor will every lecture about a particular material cover all of these properties and failure modes. However, it is a good starting point for this course, and it will provide a good background for future discussions.

I would like to point out that even for the properties that I've mentioned, there are other variations and considerations that would need to be accounted for in a more advanced class. Things like stain rate, temperature, and notch effects (also known as stress concentrations) all come into play when examining materials and designing projects. At this point though you only need to be aware that these terms exist, and have some idea about their meanings.

References

UF Class website

Github.io version of course website (Do not use this link if you are taking this course in Summer A or B.)

IPython.org (IPython is the opensource software used in the development of much of this course.)

Complete Software List

Report any problems

Issues Please report any problems that occurred during the viewing of this or any other lecture.

Alternative Reporting - Email damontallen@gmail.com